快速排序

算法

快速排序是一个非常快的排序算法，有些公司在面试基础的时候经常问到，平均情况下只有O(n log n)的时间复杂度，使得被广泛的使用在计算机科学和工程实践中。

原理

快速排序使用经典的“分治法”策略，把一个排序分解成若干个小的排序，每个小的排序完成了，那么整个大的排序认为也就完成了。

简单来说，快速排序分为3个步骤：
1，随机选取一个基准数
2，以第一步选取的基准数位基准，把要排序的数分成两份，使左边的都小于基准数，右边的都大于基准数，和基准数相等的数可以在左右两个数组中的任意一个里
3，分别对第二步生成两份数组重复1-2步骤

维基百科上的这幅动图很形象地展示了一次快速排序的执行过程：

算法实现

定义两个下标i和j，i从0的位置开始向右扫描，j从length()-1的数组队尾位置向前扫描。先从i开始，直到找到一个数比基准数大或相等，否则i++，找到后记录i的下标，然后移动j，直到找到一个数比基准数小或相等。两个数都找到后，如果此时i<=j,交换数组中i和j下标处对应的值。交换完之后i+1,j-1,然后i继续向后扫描，j继续向前扫描，当i>j时，终止。

执行完这一趟之后，会使i位置以前的数都小于或等于基准数，i位置以后的数都大于或等于基准数。

这里有一个细节，同时找到i和j之后才去交换二者，而不是像有的算法实现那样，找到i,交换基准，找到j之后再交换基准，减少了数组交换的次数和开销。

举个简单的例子，把数组{1, 12, 5, 26, 7, 14, 3, 7, 2}用快速排序进行排序。

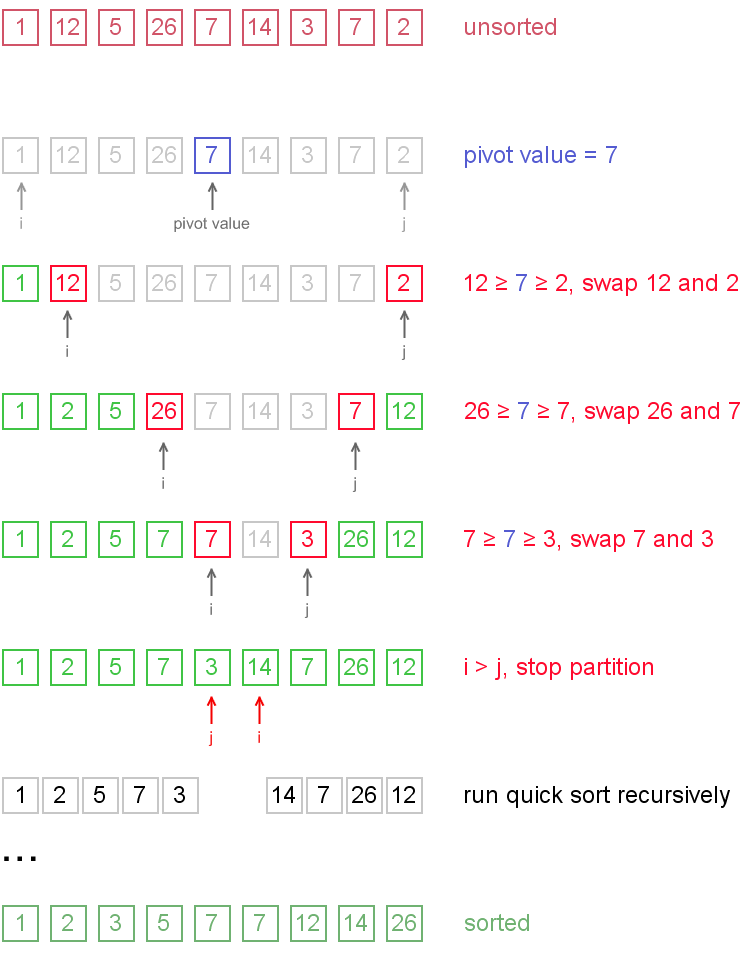
有了上面的分析，我们很容易写出相应的代码，下面是java版的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void quickSort(int arr[], int left, int right) {
    if (arr == null || arr.length == 0 || left >= right)
        return;
    int i = left, j = right;
    // pick the pivot at the middle
    int pivot = arr[(left + right) >> 1];
    // make left < pivot and right > pivot
    while (i <= j) {
        while (arr[i] < pivot && i <= j)
            i++;
        while (arr[j] > pivot && i <= j)
            j--;
        if (i <= j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
        System.out.println(Arrays.toString(arr));
    }
    // recursively sort two sub parts
    if (left < i - 1)
        quickSort(arr, left, i - 1);
    if (i < right)
        quickSort(arr, i, right);
}

总结

思考一下快速排序为什么那么快？
主要还是快速排序使用分治法有效的减少了数据间的比较次数，一趟下来把要比较的数据分成两部分，这样就避免了左边数组里的所有数和右边数组里的所有数之间再次比较，从而减小比较次数。而所有排序算法归根到底都是元素间的大小比较，快速排序能有效减小比较的次数，所以比较快。但是，由于极端情况下（基准数选的不好，导致分成的两个数组有一个为空），快速排序的时间复杂度会是O(N*N)，所以基准数的选取很重要，现在一般采用随机化函数、三数取中、中位数的中位数等的方式选择基准数。
另外强烈推荐让人眼界大开的好文：数学之美番外篇：快排为什么那样快