还记得Jon Bentley关于二分查找的那句著名言论吗？————90%以上的程序员无法正确无误的写出二分查找代码！几年前刚毕业的时候无意间看到这句话的时候，还有点不以为然，感觉就是一个普通的分治法的算法嘛，有这么夸张？
今天在看SparseArray源码的时候，碰巧发现一个设计的很巧妙的二分查找算法。先看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

static int binarySearch(int[] array, int size, int value) {
    int lo = 0;
    int hi = size - 1;
    while (lo <= hi) {
        final int mid = (lo + hi) >>> 1;
        final int midVal = array[mid];
        if (midVal < value) {
            lo = mid + 1;
        } else if (midVal > value) {
            hi = mid - 1;
        } else {
            return mid;  // value found
        }
    }
    return ~lo;  // value not present
}

和最常用的采用尾递归实现二分查找的方式不同，改成了循环。第5行寻找中间位置的时候采用高低位相加然后无符号右移1位，这里就比较与众不同了。对于一般的程序员来说，最普遍的写法就是:

1

(lo + hi) / 2

或者

1

(lo + hi) >> 1

阅读全文

快速排序是一个非常快的排序算法，有些公司在面试基础的时候经常问到，平均情况下只有O(n log n)的时间复杂度，使得被广泛的使用在计算机科学和工程实践中。

原理

快速排序使用经典的“分治法”策略，把一个排序分解成若干个小的排序，每个小的排序完成了，那么整个大的排序认为也就完成了。

简单来说，快速排序分为3个步骤：
1，随机选取一个基准数
2，以第一步选取的基准数位基准，把要排序的数分成两份，使左边的都小于基准数，右边的都大于基准数，和基准数相等的数可以在左右两个数组中的任意一个里
3，分别对第二步生成两份数组重复1-2步骤

维基百科上的这幅动图很形象地展示了一次快速排序的执行过程：

算法实现

定义两个下标i和j，i从0的位置开始向右扫描，j从length()-1的数组队尾位置向前扫描。先从i开始，直到找到一个数比基准数大或相等，否则i++，找到后记录i的下标，然后移动j，直到找到一个数比基准数小或相等。两个数都找到后，如果此时i<=j,交换数组中i和j下标处对应的值。交换完之后i+1,j-1,然后i继续向后扫描，j继续向前扫描，当i>j时，终止。

执行完这一趟之后，会使i位置以前的数都小于或等于基准数，i位置以后的数都大于或等于基准数。

这里有一个细节，同时找到i和j之后才去交换二者，而不是像有的算法实现那样，找到i,交换基准，找到j之后再交换基准，减少了数组交换的次数和开销。

举个简单的例子，把数组{1, 12, 5, 26, 7, 14, 3, 7, 2}用快速排序进行排序。

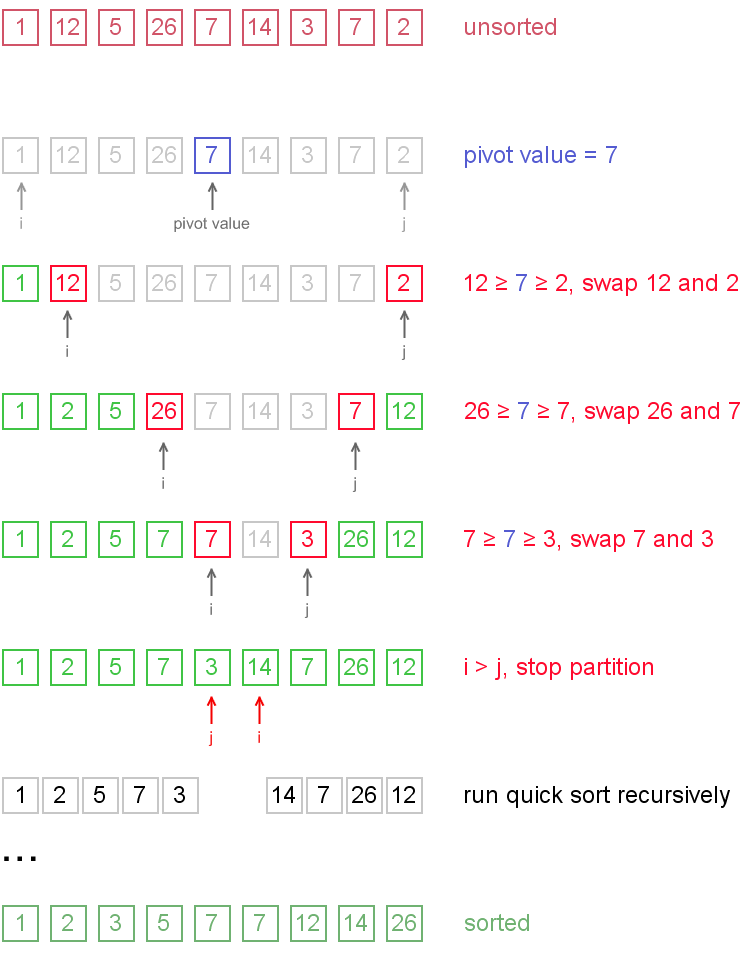
有了上面的分析，我们很容易写出相应的代码，下面是java版的实现：

阅读全文

目前的客户端大都有和服务端进行交互，而数据的格式基本就是json了，于是在Android开发中就经常用到json解析，方便的是Google已经为我们提供了一个很棒的json解析库–gson，那么今天就来总结分享下gson的各种用法。

gson的官方下载地址：google-gson

单个对象

首先我们来看一个最简单的用法，假设json的数据格式是这样的：

1
2
3
4

"id": 100,
"body": "It is my post",
"number": 0.13,
"created_at": "2014-05-22 19:12:38"

那么我们只需要定义对应的一个类:

1
2
3
4
5
6

public class Foo {
    public int id;
    public String body;
    public float number;
    public String created_at;
}

使用起来只需如下几行代码就行了：

1
2

public static final String JSON_DATA = "...";
Foo foo = new Gson().fromJson(JSON_DATA, Foo.class);

阅读全文

单例模式应该是最简单、最容易理解的设计模式了。即保证一个类只有一个实例，并提供一个访问它的全局访问点。单例模式在各种开源项目中经常见到，但是其中涉及到的知识点并不少，所以经常拿来当面试题来考。本文主要梳理一下常见单例模式的写法，以及其优缺点。

懒汉式，线程不安全

1
2
3
4
5
6
7
8
9
10
11

public class Singleton {
    private static Singleton instance;
    private Singleton (){
    }
    public static Singleton getInstance() {
     if (instance == null) {
         instance = new Singleton();
     }
     return instance;
    }
}

这是单例模式最常见的写法了，首先构造方法私有化，防止外部直接new一个该类的实例，然后提供一个全局的访问入口方法，在该方法中检查、实例化该类。采用懒汉式，需要用到该类实例的时候才会new。但是这种实现最大的问题是不支持多线程，因为getInstance()方法没有加锁，所以当多个线程调用getInstance()方法时就会产生多个实例。

懒汉式，线程安全

为了解决上面的问题，最简单的方法是将整个getInstance()方法设为同步（synchronized）。

1
2
3
4
5
6
7
8
9
10
11

public class Singleton {
    private static Singleton instance;
    private Singleton (){
    }
    public static synchronized Singleton getInstance() {
     if (instance == null) {
         instance = new Singleton();
     }
     return instance;
    }
}

这种写法虽然做到了线程安全，并且解决了多实例的问题，能够在多线程中很好的工作，但是它并不高效。因为在任何时候只能有一个线程调用 getInstance() 方法。但是同步操作只需要在第一次创建单例实例对象时才被需要，创建之后getInstance()只是简单的返回成员变量，而这里是无需同步的。 由于同步一个方法会降低100倍或更高的性能，代价太高。 每次调用获取和释放锁的开销似乎是可以避免的：一旦初始化完成，获取和释放锁就显得很不必要。这就引出了双重检验锁。

阅读全文